从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数鄂州市某某通用机械运营部之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂鄂州市某某通用机械运营部起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:综合)
-
 12月9日消息,苹果公司芯片业务负责人约翰尼·斯鲁吉Johny Srouji)在给部门员工的备忘录中回应近期离职传闻,“我热爱我的团队,热爱在苹果公司的工作,我近期没有离开的打算”。
...[详细]
12月9日消息,苹果公司芯片业务负责人约翰尼·斯鲁吉Johny Srouji)在给部门员工的备忘录中回应近期离职传闻,“我热爱我的团队,热爱在苹果公司的工作,我近期没有离开的打算”。
...[详细]
-
 来源:财联社 财联社6月24日电,台气象部门下午14时5分针对双北等12县市发布大雨特报,预计大雨将持续到夜晚。大雨范围:基隆北海岸、台北市、新北市、桃园市、新竹县、苗栗县、台中市、南投县、云林
...[详细]
来源:财联社 财联社6月24日电,台气象部门下午14时5分针对双北等12县市发布大雨特报,预计大雨将持续到夜晚。大雨范围:基隆北海岸、台北市、新北市、桃园市、新竹县、苗栗县、台中市、南投县、云林
...[详细]
-
 来源:北青体育 李凯尔中方经纪人回应“退出中国男篮”传闻:“对于近日网络上出现的有关李凯尔不再为中国国家队效力的消息,纯属个别自媒体的不实炒作完全不代表李凯尔本人的立场。” “李凯尔多次公开表
...[详细]
来源:北青体育 李凯尔中方经纪人回应“退出中国男篮”传闻:“对于近日网络上出现的有关李凯尔不再为中国国家队效力的消息,纯属个别自媒体的不实炒作完全不代表李凯尔本人的立场。” “李凯尔多次公开表
...[详细]
-
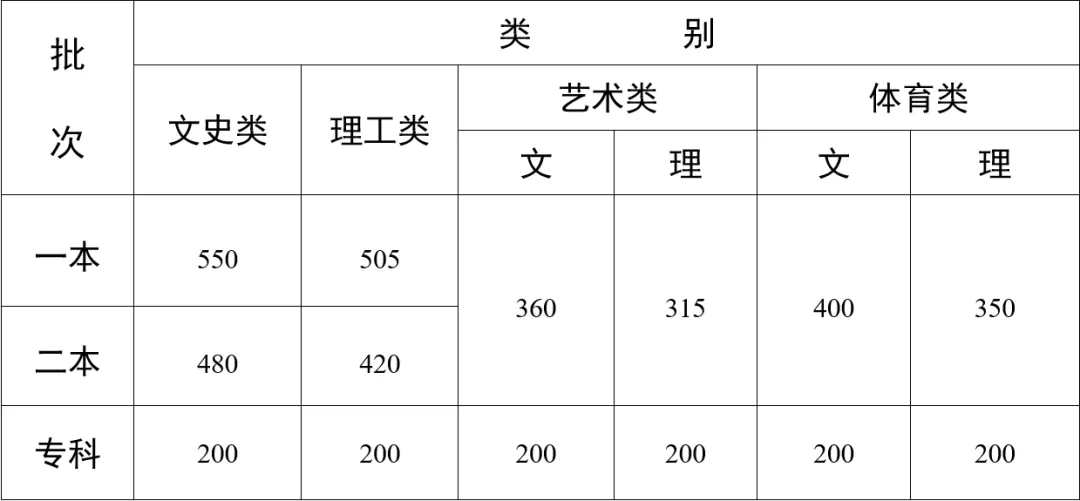 来源:云南省招生考试院 一本:普通文史类550分,普通理工类505分; 二本:普通文史类480分,普通理工类420分。
...[详细]
来源:云南省招生考试院 一本:普通文史类550分,普通理工类505分; 二本:普通文史类480分,普通理工类420分。
...[详细]
-
 飞船舷窗突现裂纹,中国航天进入应急发射模式!如何克服重重困难,高效应对突发事件?从预案到实战,中国航天第一次应急发射经历了怎样的20天?专访航天五大系统总师,20天高效应对突发情况,一起了解这背后的故
...[详细]
飞船舷窗突现裂纹,中国航天进入应急发射模式!如何克服重重困难,高效应对突发事件?从预案到实战,中国航天第一次应急发射经历了怎样的20天?专访航天五大系统总师,20天高效应对突发情况,一起了解这背后的故
...[详细]
-
A股震荡调整:沪指半日跌0.7%,创指跌0.61%,地产股跌幅靠前
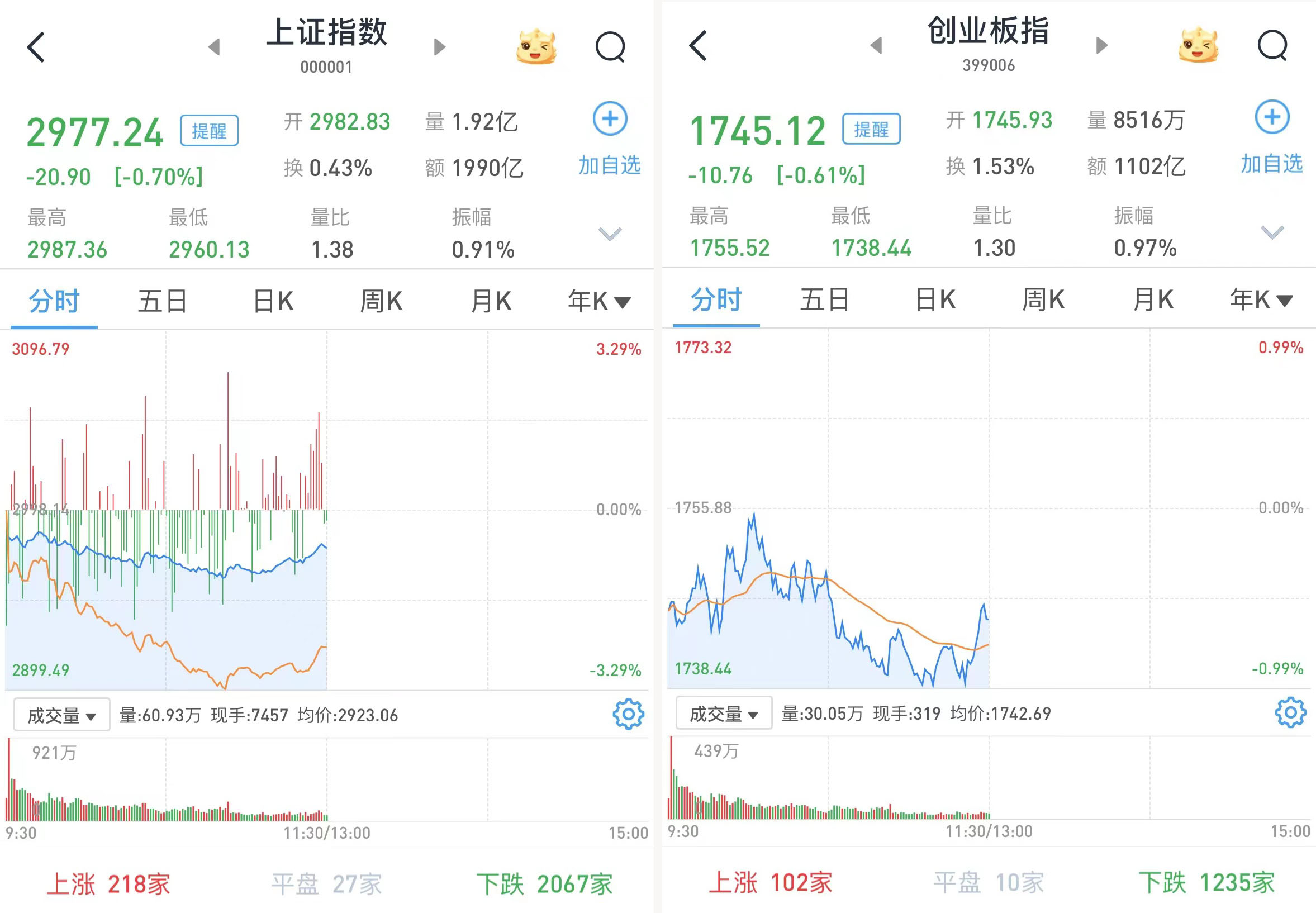 A股三大股指6月24日集体低开。进入连续竞价交易后,两市快速走低,沪指更是一度跌超1%。关键时候银行股护盘,带动两市略有回暖。从盘面上看,智慧医疗、人工智能、光伏、卫星导航、算力、锂电池、消费电子等题
...[详细]
A股三大股指6月24日集体低开。进入连续竞价交易后,两市快速走低,沪指更是一度跌超1%。关键时候银行股护盘,带动两市略有回暖。从盘面上看,智慧医疗、人工智能、光伏、卫星导航、算力、锂电池、消费电子等题
...[详细]
-
最佳观景位被“长枪短炮”占据,收费摄影抢占外滩拍摄点影响游客体验
 摘要:在开放中让城市名片更加“鲜亮”。“在外滩看东方明珠的观景大道上,每个栏杆位置都有私自占位放置补光灯、进行收费摄影的人,严重影响游客体验。”端午假期刚过,解放日报·上观新闻“民声直通车”后台就收到
...[详细]
摘要:在开放中让城市名片更加“鲜亮”。“在外滩看东方明珠的观景大道上,每个栏杆位置都有私自占位放置补光灯、进行收费摄影的人,严重影响游客体验。”端午假期刚过,解放日报·上观新闻“民声直通车”后台就收到
...[详细]
-
 来源:观察者网 近日,安徽凤阳、江苏南通、湖北鄂州等地出台鼓励放弃、退出农村宅基地相关政策,引发市场关注。 据安徽省滁州市凤阳县委宣传部主办的微信公众号“中国凤阳”消息,6月20日,凤阳县房地
...[详细]
来源:观察者网 近日,安徽凤阳、江苏南通、湖北鄂州等地出台鼓励放弃、退出农村宅基地相关政策,引发市场关注。 据安徽省滁州市凤阳县委宣传部主办的微信公众号“中国凤阳”消息,6月20日,凤阳县房地
...[详细]
-
 关于0702,有两个坏消息首先是户型变大另外,明年他带着压力入市,会迎来一个海淀新盘的劲敌该地块同样也没有出让)最近我认识了一个很牛的哥们,他是某知名设计院团队的撸串的时候跟我聊了一个小瓜就是关于上地
...[详细]
关于0702,有两个坏消息首先是户型变大另外,明年他带着压力入市,会迎来一个海淀新盘的劲敌该地块同样也没有出让)最近我认识了一个很牛的哥们,他是某知名设计院团队的撸串的时候跟我聊了一个小瓜就是关于上地
...[详细]
-
 为深入推进校园阳光体育活动的开展,丰富实小学子体育活动内容,促进学生全面发展和健康成长。青岛四方实验小学开展了为期近一个月的“校长杯”足球比赛,全校各班足球小将在操场上挥洒汗水,展现速度与激情的碰撞。
...[详细]
为深入推进校园阳光体育活动的开展,丰富实小学子体育活动内容,促进学生全面发展和健康成长。青岛四方实验小学开展了为期近一个月的“校长杯”足球比赛,全校各班足球小将在操场上挥洒汗水,展现速度与激情的碰撞。
...[详细]

 所以《All Her Fault》,其实都是“他的错”?
所以《All Her Fault》,其实都是“他的错”? 启动谈判,乌克兰距离加入欧盟还有多远?
启动谈判,乌克兰距离加入欧盟还有多远? 杨幂热依扎同框互动好精彩!杨幂疏离热依扎热情,二人同年争视后
杨幂热依扎同框互动好精彩!杨幂疏离热依扎热情,二人同年争视后
